Ⅰ. 서 론
최근 몇 년간 주택 가격은 우리 사회의 꾸준한 관심사로서 개인, 정책당국, 금융기관과 밀접한 관련이 있는 중요한 경제학적 요인으로 인식되어 왔다. 먼저, 주택 자산은 우리나라 국민 개인 자산 유형별 구성비의 68%1)를 차지할 만큼 그 비중이 매우 크다. Mills(2008)는 1970년부터 2000년 사이에 OECD 국가 내에서 발생한 20번의 주택경기침체가 19번의 경기 침체로 이어졌다는 사실을 통해 정책 당국의 관점에서 주택 경기가 국가 경기와 밀접한 관계에 있는 매우 중요한 요소임을 보였다. Crawford(1995)는 주택가격의 변동성이 주택대출 채무불이행과 조기대출상환을 결정하는 주요 요인이며, 특히 주택담보비중이 높은 금융기관에 있어서도 매우 중요하다는 사실을 보였다. 즉, 주택 가격은 단순히 주택 경기뿐만 아니라 국가 경제 전반의 안정화와 관련 정책 수립에 있어 중요한 요인으로 볼 수 있다.
주택 가격 예측 연구는 미래 주택 가격에 대한 불확실성을 줄이고, 관련된 정책적 시사점을 도출하는데 그 의의가 있다. 이에 다수의 연구자들과 연구 기관들은 보다 간단한 구조로 오차 범위를 줄일 수 있는 계량경제학적 모델들을 개발하고자 다양한 연구 모델과 방법론을 제시하였다. 그러나 기존의 연구에서 사용하고 있는 전통적인 계량 경제학적인 접근 방식인 VAR이나 ARIMA 모형에는 두 가지 구조적인 한계가 존재한다. 먼저, 예측력과 분석 구조의 트레이드오프(trade-off) 관계 때문에 주택 가격 예측 변수들의 수가 늘어나고 더 다양해질 경우, 예측력은 높아지지만 동시에 분석 구조가 복잡해지는 문제가 발생한다. 이는 분석을 더욱 어렵게 할 뿐만 아니라, 오히려 분석력을 떨어트리는 과적합(overfitting) 문제를 야기할 수 있다. 또한, 기존의 방법론은 사전에 모델 자체의 불확실성을 반영하지 못하기 때문에 예측력 향상에 한계가 있다. 즉, 연구자의 주관이 반영된 특정 모델에서 분석을 시작할 경우, 모델 고유의 불확실성을 안고 있어 보다 정교한 예측에 어려움이 있다.
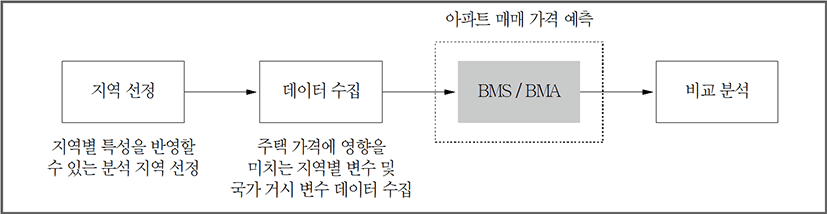
본 연구는 이러한 문제에 착안해 연구의 목적을 크게 두 가지로 구성하였다. 먼저, 기존의 접근 방식이 아닌 베이지안 방법론을 이용해 모델의 복잡성 문제와 예측력을 개선할 수 있는 연구 모델을 도출해내고자 한다. 베이지안 이론을 기반으로 하는 Bayesian Model Selection(BMS)과 Bayesian Model Averaging (BMA)은 모델의 불확실성을 반영한 분석이 가능할 뿐만 아니라, 기존의 방법론보다 많은 정보를 활용하기 때문에 예측력 개선에 있어 강점이 있다. 이에 본 연구에서는 위 베이지안 분석 방법론을 이용해 추정한 아파트 실거래가지수와 기존의 분석에서 주로 사용되는 AR모형을 통해 추정한 아파트 실거래가지수를 실측치와 상대 비교하여 보다 나은 예측 모형을 선정할 것이다.
또한, 본 연구는 분석 대상의 다변화를 위해 서로 다른 지역을 분석 대상으로 선정함으로써 지역적 특색을 반영한 분석 결과를 도출하고자 한다. 아파트 가격과 같은 부동산 가격은 국가별 거시적 요인 혹은 정책적 요인뿐만 아니라 지역별 환경적 요인에 의해 그 변화의 정도와 크기가 다르게 나타난다. 이처럼 지역별 차이는 분석에 있어 매우 중요한 판단의 요소로 볼 수 있으며, 본 연구에서는 서울과 부산 두 지역을 선정하여 각각의 경우에 적합한 분석 결과를 보일 것이다.
Ⅱ. 선행 연구
주택 가격 연구는 주택 가격 변동의 원인을 설명하고 주요 결정 요인을 분석하거나 이러한 이론적 배경을 토대로 향후 주택 가격을 예측하는데 연구의 목적을 두고 있다. 특히, 미국의 서브 프라임 모기지 사태 이후 형성된 주택 가격의 중요성과 주택 가격 변동에 대한 문제의식은 주택 가격에 대한 새로운 이해와 접근 방식의 필요성을 야기하였으며, 이에 많은 연구들은 이를 위해 다양한 분석 방법을 이용해 대안을 제시하고 있다.
주택 가격은 개별 주택의 헤도닉적 특성과 국가의 정책 및 거시 경제적 요인들, 수요와 공급 조건, 그리고 지역별 경제 요인들 등 다양한 요인들의 효과에 의해 결정된다. 주택 가격의 헤도닉 특성은 주택에 내제되어 있는 관찰되지 않는 특성들을 의미하며 기존의 연구들은 대지권, 지리적 특성, 토지와 건물의 배분 비율, 용적률, 조망권, 남향 여부, 학군 등 다양한 요소들을 이용해 주택 가격과의 연관성과 그 효과를 분석하였다(임병군, 2006; 정성용, 2009). 그러나 주택 가격의 헤도닉 가격 모형에는 데이터 확보뿐만 아니라, 변수의 범주 선정, 모형 설정 및 모형 추정에 구조적 한계가 있다(이용만, 2008). 특히 지역의 특성에 따른 이분산과 변수 선정 시 발생할 수 있는 변수누락(omitted variables) 문제는 왜곡된 결과로 이어질 수 있기 때문에 면밀한 분석이 요구된다. 이에 윤효묵 외(2013)는 위계적 선형모형으로 서울 지역의 주택 가격을 분석해 과거보다 주택의 지역적 특성이 개별 특성보다 영향력이 더 큼을 보인바 있다.
주택 정책과 관련해서 최차순(2010)은 부동산시행정책을 계량화한 정책 변수를 사용하여 부동산 정책이 부동산 가격의 변동성에 인과하고, 정책에 대한 반응이 지역 및 아파트매매 및 전세시장, 토지매매시장별로 다름을 보였으며, 함종영 외(2012)는 부동산 정책과 정책시장동향이 단기간에서 인과관계가 성립하지 않음을 통해 정책변수의 내생성 문제를 강조하였다. 노영학 외(2012)는 주택관련정책들과 거시경제변수들이 주택가격지수에 미치는 영향 정도를 다중 회귀 분석을 통해 주택가격지수가 주택관련정책보다는 거시경제변수들 특히 경기선행지수와 종합주가지수에 크게 영향을 받는다는 결론을 도출하였으나, 정권 교체시 발생하는 시장의 불안전성을 반영하지 못해 다소 현실성이 떨어진다는 한계를 드러냈다. 이처럼 주택 정책이 미치는 효과를 제대로 분석하기 위해서는 시기, 지역 및 시장을 고려한 정책의 정교한 모형화뿐만 아니라 내생성과 같은 여러 요소들을 고려해야 한다는 문제가 발생한다.
주택 가격 연구에서 사회 경제학적 변인들은 주로 GDP, 실업률, 소비자 물가지수, 시장금리와 같은 국가 단위 혹은 지가변동률, 거래 실적 등과 같은 지역 단위 경제 변수들로 구성된다. 먼저 거시 경제변수 관련해서 Dolde and Tirtiroglu(2002)는 주택 가격이 수입 증가, 인플레이션, 이자율 등의 변수와 관련 있음을 보였으며, 김현재(2011)는 실업률과 같은 변수 또한 주택 가격에 영향을 미친다는 결과를 제시하였다. 즉, 사회경제학적 요인들은 주택 가격 분석에 있어 매우 중요하며, 이에 보다 다양한 지역을 대상으로 하는 연구에서는 국가 단위 혹은 지역 단위의 사회 경제학적 변인들이 주로 사용되고 있다.
그러나 이러한 거시 경제 변수들은 시기와 그 지역에 따라 그 효과가 다르게 나타났는데, 김윤영(2012)은 금융위기와 외환위기 전후로 구분한 분석을 통해 거시경제 변수가 주택 가격에 유의미한 영향을 미침을 보였으며, 한경수(2011)는 지역별로 거시변수가 주택 가격에 미치는 효과가 다르다는 결과를 도출하였다. 이는 주택 가격 분석에 있어 거시 경제 변수와 지역적 요인들을 다양한 기간에 걸쳐 고려해야한다는 것과 이러한 효과의 차이가 분석과 모형 선정에 어려움을 야기한다는 사실을 시사한다.
주택 가격 예측 연구는 주택 가격이 과거 가격에 의존해 변동한다는 사실을 기반으로 시계열 분석을 이용해 미래 주택 가격을 예측한다. 이에 기존의 연구에서는 VAR이나 ARIMA와 같은 연구 모형의 오차 범위 비교를 통해 보다 나은 예측력을 보이는 모형을 도출하기 위한 시도들이 이루어졌다(Case and Shiller, 1989; 이영수, 2014). Son et al.(2003)은 ARMA와 VAR를 비교 분석하는 연구에서 부동산가격 예측모형으로 실질 GDP 성장률과 회사채 수익률을 고려한 VAR모형과 ARMA모형과의 비교분석을 통해 VAR모형의 예측력이 우수함을 보였다. 손정식 외(2002)는 이론적으로 모순이 없고 인과관계 분석 결과에서 유의미한 것으로 나타난 거시변수들로 VAR 예측 모형을 구축해 시장 여건 변화를 반영한 새로운 부동산 가격 예측 모형 분석을 시도하였으며, 그 결과 VAR 모형의 예측력이 ARMA 모형보다 상대적으로 우수하다는 결론을 도출하였다. 이와 유사한 연구로 한국주택금융공사(2012)에서 실시한 아파트 실거래 가격지수 예측 연구 결과에 따르면 예측 오차를 최소화하는 측면에서는 ARMA가 VAR보다 나았으나, 주택경기 급변동시에는 거시경제 변수를 반영하는 VAR이 나은 것으로 나타났다.
이처럼 기존의 모형들은 경우에 따라 각각의 장단점이 있는 것으로 나타났으나, 여전히 예측력에서의 한계를 보였으며, 이에 이를 개선하기 위한 새로운 예측 모형들이 제시되었다. 먼저, ARMA를 이용한 주택 가격 예측 연구에서 Kim(1998)과 윤주현 외(2000)는 주택 가격의 단기예측모형으로 ARMA모형과 상태공간모형의 결과를 비교 분석하여 상태공간모형이 ARMA모형보다는 예측력에 있어 보다 우수하다는 결론을 도출하였다. Lee and Lee (2009)는 ARMA모형과 인공지능망 모형으로 서울시 주택가격지수를 분석하여 두 모형 간에 통계적으로 유의한 차이는 없으나 예측력에 있어서는 신경망 모형이 우수하게 나타났음을 보였다. ARMA, IGARCH, 국면전환(RS), 비관측요인(UC)과 같은 단일변수 시계열 모형들의 주택가격 예측력을 비교한 연구 결과에 따르면, 표본 외 예측의 경우에 비관측요인 모형이 국면전환 모형의 예측력보다 크게 낮은 것으로 나타났다(이영수, 2014).
또한, 전통적인 통계학적 접근 방식이 아닌 베이즈 이론을 기반으로 하는 Bayesian Model Selection(BMS), Bayesian Model Averaging (BMA)가 모델 선정의 불확실성 문제를 개선한 연구 방법론으로서 주목받고 있다. Bates and Granger(1969)에 의해 최초로 소개된 BMS와 BMA 모형은 이후 다양한 연구를 통해 그 예측력이 입증되었다. 특히 BMA 모형은 인플레이션(Engle, Granger and Kraft, 1984; Wright, 2008), 통화공급(Figlewski and Urich, 1983), 환율(Bilson, 1983), 그리고 GDP 성장률(Fernández et al., 2001)을 예측하기 위한 시계열 분석 연구로서 사용되었으며, 주택 가격 예측과 관련해서는 미국(Dua et al., 1999), 스위스(Stadelmann, 2010), 남아프리카(Gupta et al., 2008) 등을 대상으로 한 다양한 실증 분석이 이루어졌다.
이에 본 연구는 각 모델 선정의 불확실성을 고려한 BMS, BMA를 이용하여 주택 가격 예측 모형을 도출해 내고자 한다.
Ⅲ. 데이터 및 분석
본 연구에서는 주택가격 예측의 지표로 매월 한국감정원에서 아파트 실거래 가격자료를 기초로 작성, 발표하는 서울, 부산 지역의 아파트 실거래가격지수를 선정하였다. 아파트 실거래가격지수는 2006년 1월을 기준시점(100)으로 지수산정기간 중 거래신고가 2번 이상 있는 동일 아파트의 실거래가격 자료에 한하여 가격변동률을 산출한 값으로서, 아파트의 거래가격수준 및 변동률을 파악하여 정확한 시장동향 정보를 제공한다는 면에서 널리 사용되고 있으나 근본적으로 지수 산정방식에 있어 두 가지 큰 문제점을 안고 있다. 먼저, 동일한 아파트의 실거래가격이 반복적으로 관측되지 않는데서 발생하는 자료 활용의 비효율성 문제가 있다. 동일 조건의 실거래가격이 반복적으로 관측되지 않을 경우, 지수산정에서 해당 자료는 배제되어 결과적으로 가격지수의 안정성에 부정적인 영향을 끼칠 수 있다. 두 번째로는 매 시점마다 완벽하게 동일단지, 동일평형의 가격 자료를 매번 얻을 수 없어 야기되는 표본추출 오류의 문제가 있다. 이로 인해 매 시점 관측되는 아파트의 빈도수 차이에 따른 표본 편의가 발생하고 이는 곧 지수의 신뢰도를 낮추는 요인으로 작용할 수 있다. 이와 관련하여 이창무 외(2008)는 위의 문제들을 해결하고자 매년 아파트 가치를 나타내는 시세가격을 활용하여 기존 반복매매지수 산출방식에서 배제되었던 실거래가격자료를 반영한 아파트 실거래가격지수를 재 산정하였고, 그 결과 자료 활용 측면에서 약 18.6%의 향상이 가능함을 보였다. 그러나 이러한 접근 방법이 자료 활용의 효율성 측면에서 큰 효과를 보였음에도 불구하고, 아파트 실거래가격지수 변동에는 큰 차이를 보이지 못한 것으로 드러났다. 이에 본 연구에서는 별도의 아파트 실거래가격지수 재 산정 없이 한국감정원에서 발표하는 아파트 실거래가격지수를 변형 없이 그대로 사용하였다.
독립변수로는 2007년 1월부터 2014년 12월까지 통계청과 한국은행에서 제공하는 지가변동률, 실업률, 아파트 건설실적, 아파트 거래현황, 소비자 물가지수, 시장금리, 주택담보대출금리, GDP(실질, 명목), 전산업생산지수, CD금리 등 총 11개의 거시경제지표 및 부동산 관련지수를 사용하였다. 위의 독립변수는 크게 공급변수와 수요변수로 구성된다. 먼저, 공급변수에는 아파트 공급 측면에서 아파트 매매 가격에 영향을 주는 변수들로 건설경기의 효과를 반영하고 있는 아파트 건설실적과 아파트 건설에 필요한 토지 가격 변동성을 반영한 지가변동률이 해당된다. 반면, 수요변수로는 아파트 수요 측면에서 아파트 매매 가격에 영향을 주는 변수로서 아파트 거래현황, 실업률, 소비자 물가지수, 시장금리, 주택담보대출금리, GDP(실질, 명목), 전산업생산지수, CD금리를 선정하였다. 전반적으로 소득의 영향이나 시중금리의 움직임을 반영하기 위해 GDP, 소비자물가지수, 전산업생산지수, 실업률, CD금리를 사용하였고, 주택 가격과 은행대출간의 양의 상관관계에 관한 연구 결과를 토대로(박연우 외, 2012) 주택담보대출금리를 추가로 사용하였다. 지역의 차이를 반영하기 위해 위 변수들 중 지가변동률, 실업률, 아파트 거래실적은 지역단위로 구성하였으며, 나머지 변수들은 전국단위 변수로 설정하였다.
베이즈 이론은 이전의 경험과 현재의 정보를 토대로 특정 사건의 확률을 추론하는 통계적 접근 방법으로서, 빈도주의 접근법과 확률의 해석을 달리한다. 빈도주의 접근법이 관찰에 의한 특정 사건의 객관적인 확률에 초점을 맞춘다면, 베이즈주의 접근법은 관련 정보에 근거한 특정 사건의 주관적인 확률에 중점을 두고 있다. 이를 기반으로 하는 베이즈 추론은 추정하고자 하는 대상()에 대한 사전 지식(혹은 사전 확률, prior probability)을 새로운 정보()로 업데이트해 나가면서 이에 대한 새로운 확률 분포(혹은 사후확률분포, posterior probability)를 만들어내는 알고리즘을 따른다. 본 연구에서 사용하고자 하는 BMS, BMA 모형은 초기의 모델 선정까지 고려한 분석으로 총 32기의 데이터 중 16기까지의 데이터를 토대로 17기부터 32기까지의 아파트 매매가격지수를 예측하였으며, 전체적인 분석의 구성은 사후 확률 계산, 모델 선정, 예측의 3단계로 구성하였다.
각 모델들은 변수들의 조합들을 통해 구성해 본 일종의 개별 수학적 시나리오라고 볼 수 있다. 본 연구에서 사용하는 BMS, BMA 모형은 총 11개의 설명변수로 조합 가능한 개, 즉 2,047개 모델들의 사후 확률을 계산한 결과를 사용하고 있으며, 이는 기본적으로 2단계 분석을 거쳐 진행되었다. 먼저, 2,047개의 모델에 대해서 1기부터 16기까지에 걸친 데이터를 토대로 의 우도 확률 값을 계산하였다(식(1)). 본 연구에서 는 주택가격예측모형의 모수, M은 모델, D는 이를 업데이트하는데 사용되는 데이터를 의미한다.
그런 다음, 1단계에서 구한 각 모델의 우도 확률 값을 이용해 모델의 사후 확률 을 추정하였다(식(2)). 모델의 사후 확률은 데이터가 주어졌을 때 특정 모델이 참이 될 확률을 의미하며 앞에서 구한 우도 확률 값 과 사전확률 값 의 곱으로 풀어 쓸 수 있다. 여기서 사전확률 은 연구자의 주관적인 정보가 반영된 확률로서 연구자가 가진 정보에 따라 각각의 모델에 서로 다른 확률을 부여할 수 있다.
이를 토대로 BMS 방법론은 각 변수들의 모든 조합을 고려한 모델들의 사후 확률인 결과 값 중 확률이 가장 높은 모델로 계산을 수행하였으며, BMA는 사후 확률이 큰 다수의 모델들을 선정하여 가중 평균한 값을 도출하는 방식을 사용하였다. 여기서 BMA의 경우, 수십, 수백 개의 모델들 중에서 최적의 모델들을 선정하여 가중 평균을 하기 위해서는 일정한 논리적인 기준이 필요하며, 본 연구에서는 Madigan and Raftery(1994)이 제시한 Occam’s Window를 적용하였다. Occam’s Window는 총 두 단계로 첫 번째 단계에서는 가장 확률이 높은 모델의 확률 값을 기준으로 C 값 이상이 되는 모델들을 선정하였으며, 아래 수식과 같이 해당 조건에 포함되지 않은 사후확률의 모델을 고려대상에서 제외시켰다(식(3)). 상위 확률 분포의 기준값을 의미하는 상수 C는 연구자의 직관에 따라 달라질 수 있지만, Jeffreys(1961)는 10과 100사이의 숫자를 사용하길 권하고 있어 본 연구에서는 기존의 연구에서 대체적으로 많이 쓰이는 세 가지 경우(10, 20, 30)를 설정하여 C값에 대한 민감도를 확인하였다.
Occam’s Window의 두 번째 단계에서는 1단계에서 선정한 모델들 내에서 모델 내 변수가 더 많은 하위 모델들을 제거하였다. 즉, 일차적으로는 높은 확률의 모델을 우선으로 이와 동일한 변수를 포함하고 있는 더 복잡한 모델들을 제거함으로써, 보다 높은 확률을 갖는 단순한 모델들로 최종 상위 모델들을 구성하였다(식(4)).
앞서 초기에 도출한 최상의 모델과 Occam’s Window를 통해 도출한 상위 모델들 정보를 이용해 BMS와 BMA 수식을 식(5)와 식(6)과 같이 구성하였다. 아래 식에서 k는 Occam’s Window를 만족하는 모델들이며, 그 중 BMS에서 사용된 는 사후 확률이 가장 큰 최상의 모델을 의미한다.
BMS:
BMA:
2007년 1분기부터 2010년 4분기까지의 데이터로 도출해낸 위의 정보들과 Karman Filter를 이용하여 2011년 1분기부터 매기수마다 정보를 업데이트하여 아파트 실거래가지수를 예측하였다. Kalman Filter는 항법, 제어 분야 등에서 많이 쓰이는 선형적 통계 예측 수단으로 크게 예측과 업데이트 두 단계로 구성되어 있다. 예측 단계에서는 관심의 대상인 상태변수와 상태변수의 공분산을 예측하는데 식(7)과 식(8)과 같이 나타낼 수 있다. 이렇게 t-1기의 자료를 바탕으로 예측한 , 값은 t기의 관측 자료들을 반영하여 , 로 바뀌는 업데이트 단계를 거치게 되며, 이 후 t기는 t+1기가 되어 똑같은 알고리즘을 반복한다.
State estimation:
Covariance estimation:
예를 들어 서울지역의 2011년도 1분기에 해당하는 아파트 실거래가지수를 예측을 위해 첫 번째 단계에서는 예측 단계로 그 전 분기인 2010년도 4분기의 아파트 실거래가지수 및 거시경제변수를 이용하여 2011년도 1분기에 해당하는 상태변수와 공분산을 예측하였다. 그런 다음, 업데이트 단계로 실제로 관측된 2011년도 1분기의 아파트 실거래가지수를 이용하여 앞의 상태변수 및 공분산을 업데이트하여, 매 주기마다 이러한 알고리즘을 반복하며 예측모형을 보정하였고, 이를 이용해 총 16개의 관측치를 예측하였다.
BMS와 BMA를 적용하여 구한 모델의 예측력을 비교하기 위해 ARIMA(Autoregressive Integrated Moving Average) 모형을 이용하였다. ARIMA 모형은 과거의 관측치와 오차항이 설명변수로 쓰이는 모형으로 비선형적인 시계열 자료를 분석하는데 주로 사용된다. 주택가격예측 연구에서도 모형의 간편함과 정확성 때문에 단기예측에 활용되었으며(Guo, 2012), 다른 예측모형의 비교 대상으로도 많이 쓰이고 있다(Vishwakarma, 2013; Kouwenberg and Zwinkels, 2014; Bork and Moller, 2015). 본 연구에서는 BMS, BMA와 동일하게 서울지역과 부산지역의 2007년 1분기부터 2010년 4분기까지의 데이터를 가지고 ARIMA 모형을 도출하였다.
먼저, 자료의 계절성을 확인하기 위해 다중비교와 분산분석(ANOVA; analysis of variance)을 실시했다. 그 결과 서울 지역의 경우 분기별로 평균과 분산 값의 차이가 미미하였으며, 부산의 경우 1분기에서 4분기로 갈수록 평균과 분산이 높아지고 있는 것으로 드러났다(표 2). 하지만, 통계적으로 분기별 지수의 차이는 유의하지 않는 것(p-value = 0.8773(서울), 0.8322(부산))으로 나타났다(표 3).
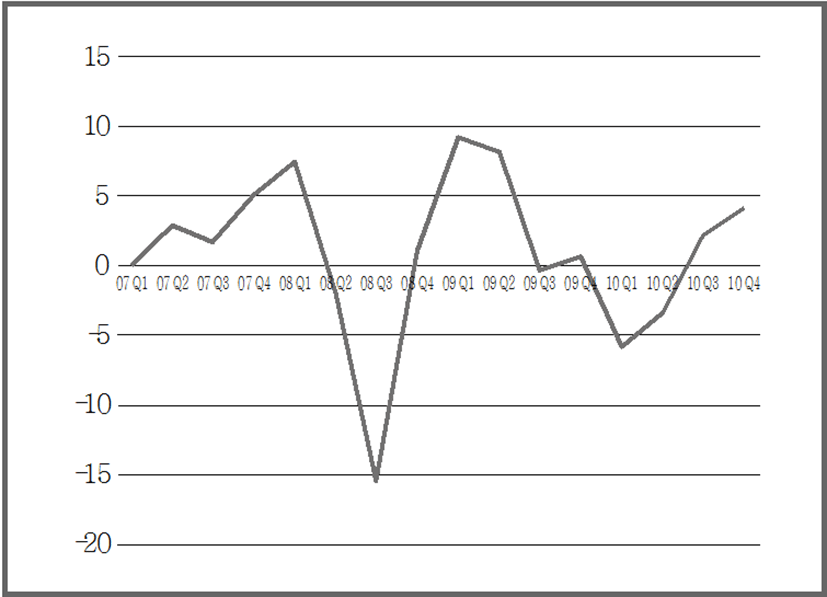
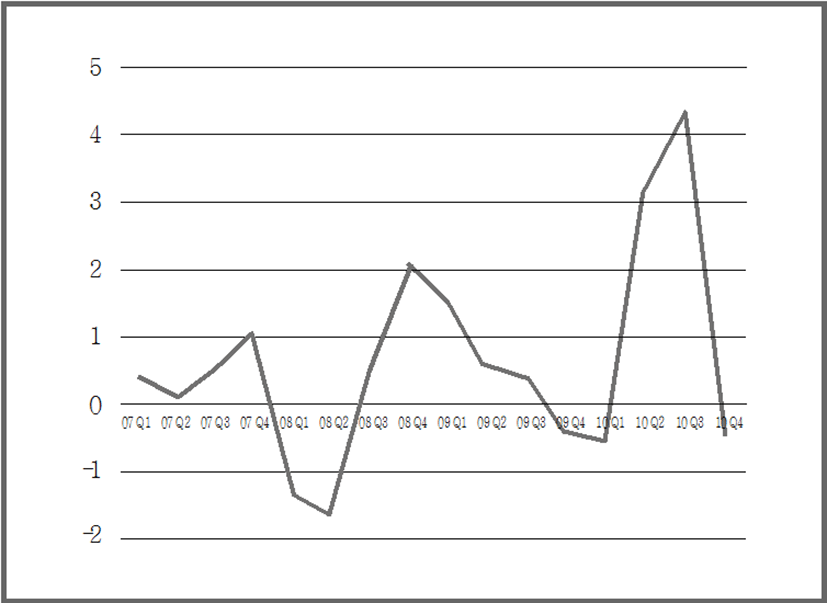
그 다음 자료의 정상성을 확인하였다. 정상성은 ARIMA 분석의 기본 조건이며, 평균이 일정하고, 상수인 분산이 존재해야하며, 두 시점사이의 자기 공분산은 시차에만 의존해야 한다는 특징이 있다(송경재 외, 2005). 단위근 검정(Unit root test)을 통해 추세를 추정한 결과, 서울, 부산 지역 모두 추세가 존재함을 확인하였다(p-value=0.7478(서울), 0.9145(부산)). 두 지역 모두 추세를 제거하기 위해 순차적으로 차분(Differencing)을 적용하였다. 서울 지역의 경우, 1차 차분을 통해 정상시계열을 얻을 수 있었으며(그림 2), 부산 지역의 경우 2차 차분을 통해 안정적인 시계열을 얻을 수 있었다(그림 3).
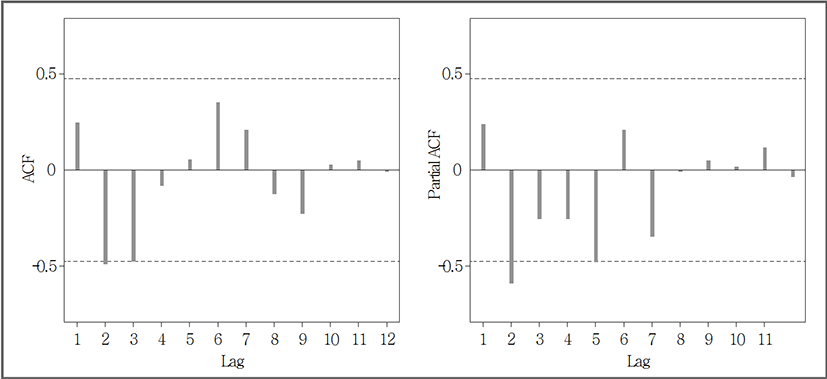
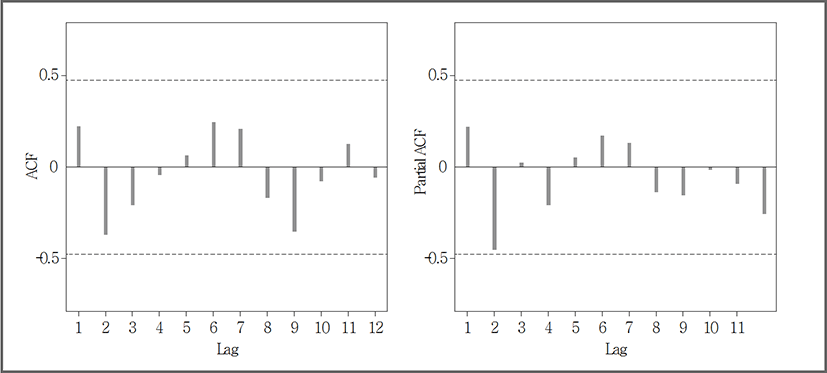
마지막으로 ARIMA 모형의 식별을 위해 자기상관계수(ACF; Auto-Correlation Function)와 편자기상관계수(PACF; Partial Auto-Correlation Function)를 이용하였다. <그림 4, 5>에서 보이는 바와 같이 서울, 부산 지역에서 ACF와 PACF는 모두 점차 진폭이 축소되는 사인 곡선의 파동을 나타내고 있으며, 유의미한 시차가 나타나지 않았다. 이는 <표 4>의 결과에서도 알 수 있듯이 두 지역 모두 ARMA(p,q) 모형의 p, q값이 0을 나타내고 있음을 알 수 있다.
위 결과들을 최종적으로 종합해본 결과 서울지역에서는 ARIMA(0,1,0) 모델이, 부산지역에서는 ARIMA(0,2,0) 모델이 선정되었다.
위에서 구한 ARIMA 모형과 함께 BMS, BMA 모형의 예측력을 비교하기 위해 RMSPE (Root Mean Square Prediction Error) 값과 Average Rank 값을 사용하였다. RMSPE 값은 관측치와 예측치 차이의 표준편차로 모델의 정확성을 비교하는데 쓰였으며, Average Rank 값은 매 예측 시점마다 가장 예측이 우수한 모델에 순위를 매겨 평균한 값으로 이를 통해 예측기간 동안 가장 선호된 모형을 도출하여 비교하였다. 또한 BMS, BMA 모형에 쓰인 적정 변수의 개수를 계산함으로써 도출된 모델을 평가하는데 객관적인 자료로 활용하였다.
Ⅳ. 분석 결과
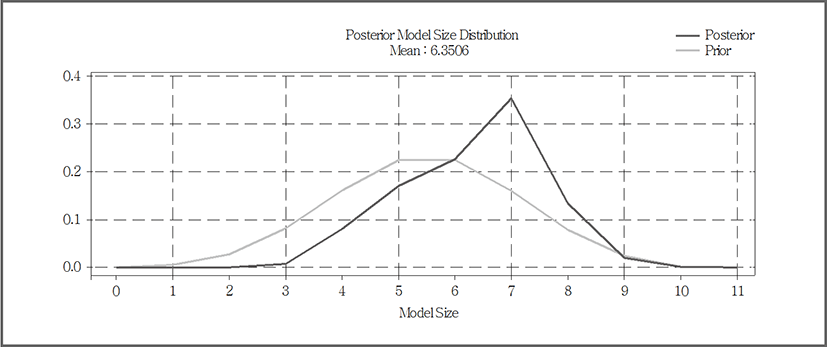
서울지역에서는 평균적으로 사후모델에 약 6.3506개의 변수가 사용되었을 때 확률이 가장 높은 것으로 나타났다(그림 6). Occam’s Window를 만족하는 사후모델로는 C값이 10인 경우, 총 5개가 선정되었으며, C값이 20, 30인 경우에 총 7개의 동일한 모델이 선정되었다. 그 중 지가변동률(서울), 소비자물가지수, 시장금리, 주택담보대출금리, CD금리를 변수로 사용하는 모델 400이 5.64%의 확률로 최상의 예측 모델로 뽑혔다(표 5). 그 외에 다른 상위 모델에서는 지가변동률(서울), 소비자물가지수, 시장금리, 주택담보대출금리, GDP(명목), GDP(실질)들의 조합이 포함되어 있는데, 특히 서울시의 경우 아파트 실거래가지수 예측에서 수요변수들이 중요한 역할을 차지하고 있음을 확인할 수 있다.
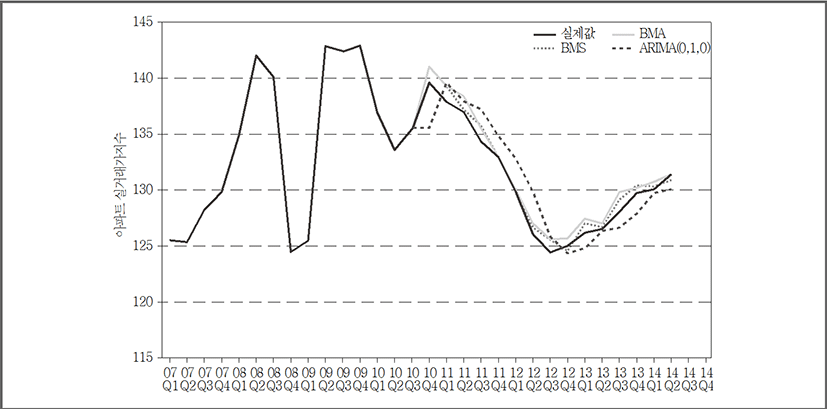
이를 이용해 2011년 1분기부터 2014년 4분기까지 서울시의 아파트 실거래가지수를 표본 외 예측(Out-of-sample prediction)한 결과를 <그림 7>과 같이 그래프로 나타내었다. 기본적으로 분석 기간 내 서울지역의 아파트 실거래가지수를 살펴보면, 2006년과 2013년 사이에 지수 값의 변동 폭이 비교적 큰 것을 확인 할 수 있다. 특히 2008년 3분기부터 2010년 4분기 사이에 등락이 심한 것을 볼 수 있는데 이는 2008년부터 시작된 미국 발 서브프라임 모기지 사태에 의한 효과로서, 우리나라의 경제침체와 국민들의 소비심리 위축에 영향을 줘 부동산 시장에도 악영향을 끼친 것으로 보인다. 이러한 현상은 앞서 수요 변수들이 주요 모델들의 변수로 사용되었다는 본 연구의 결과와 부합한다고 볼 수 있다. BMS, BMA와 더불어 ARIMA(0,1,0) 간의 예측력을 RMSE (Root Mean Square Error)값으로 비교해본 결과, BMS와 BMA는 각각 0.747, 0.967 (0.937)로 2.021의 값을 보인 ARIMA(0,1,0)보다 적은 오차 범위로 예측하였으며, 그 중에서는 BMS가 가장 우수한 예측력을 보이는 것으로 나타났다(표 6). 또한 Average Rank값으로 세 모델의 예측력을 비교해본 결과, BMS가 1.3의 값으로 전 구간에 걸쳐 가장 선호된 모델로 선정되었다. 이러한 결과는 최적의 변수 개수가 6.3506개라는 앞의 결과에 근거하여 변수의 개수가 5개인 BMS가 8개 변수를 고려하고 있는 BMA보다 적합한 모델임을 알 수 있었다.
| BMS | BMA | ARIMA(0,1,0) | ||
|---|---|---|---|---|
| C=10 | RMSE | 0.747 | 0.967 | 2.021 |
| Average Rank | 1.3 | 2 | 2.7 | |
| C=20, 30 | RMSE | 0.747 | 0.937 | 2.021 |
| Average Rank | 1.3 | 2 | 2.7 |
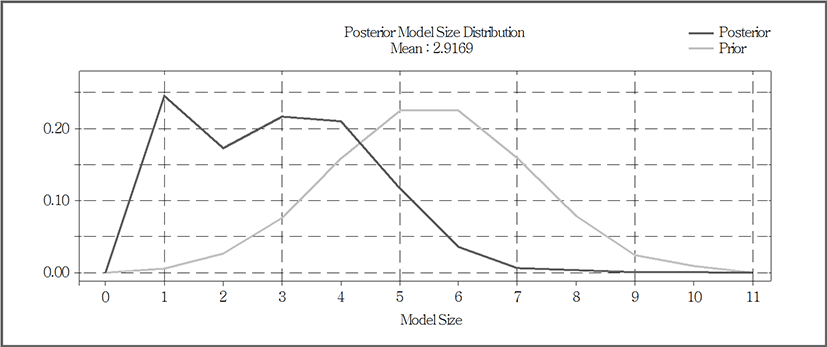
부산지역의 경우 상대적으로 서울보다 적은 2.9169개의 변수들로 이루어진 모델들의 사후 확률이 가장 높은 것으로 나타났다(그림 8). C값이 20, 30인 경우에는 총 2개의 모델들이 Occam’s Window를 만족하는 것으로 나타났으며, 그 중 GDP(명목)을 사용하는 모델 10이 최상의 예측 모델로 선정되었다(표 7). 그 외의 모델 448에서는 지가변동률(부산), 시장금리, GDP(실질)이 포함되었다. C값이 10인 경우에는 모델 10 하나만 Occam’s Window를 만족한 것으로 나타났다.
| C값 | 모델명 | 사용된 변수 | 확률 |
|---|---|---|---|
| 10 | 10 | GDP(명목) | 0.2424471 |
| 20, 30 | 10 | GDP(명목) | 0.2424471 |
| 448 | 지가변동률(부산), 시장금리, GDP(실질) | 0.0167098 |
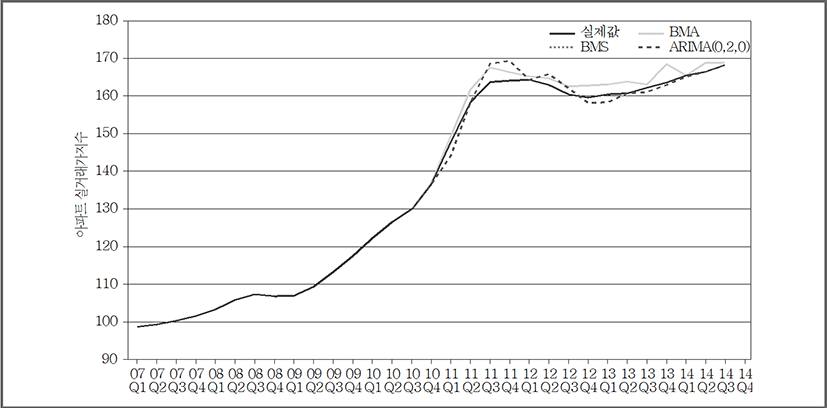
마찬가지로 위 모델들을 이용해 부산시의 아파트 실거래가격지수를 표본 외 예측한 결과를 <그림 9>에 나타내었다. 부산의 경우, 동일기간 내 아파트 실거래가지수의 변동이 서울에 비해 심하지 않고 꾸준히 상승함을 확인할 수 있는데, 예측 결과 역시 서울의 결과보다 실제값을 보다 잘 예측함을 보였다. 각각의 예측력 비교를 위해 RMSE를 비교한 결과, 서울과 달리 BMA는 2.054(2.051), BMS는 2.054, ARIMA(0,2,0)는 2.350 순으로 BMA의 예측력이 가장 뛰어난 것으로 나타났다. Average Rank값을 통해서는 ARIMA(0,2,0)이 1.4(1.8)의 값으로 전 구간에 걸쳐 예측력이 우수한 것으로 나타났다(표 8). 부산지역에서도 동일하게 적정변수가 2.9161개라는 사실에 근거하여 4개의 변수로 구성된 BMA가 1개의 변수로만 구성된 BMS보다 더 적합한 모델임을 확인할 수 있었다.
| BMS | BMA | ARIMA(0,1,0) | ||
|---|---|---|---|---|
| C=10 | RMSE | 2.054 | 2.054 | 2.350 |
| Average Rank | 1.6 | 1.6 | 1.4 | |
| C=20, 30 | RMSE | 2.054 | 2.051 | 2.350 |
| Average Rank | 1.9 | 2.3 | 1.8 |
Ⅴ. 결 론
본 연구는 기존의 방법론을 사용했을 때 발생되는 모델 선정의 불확실성 문제를 반영한 BMS, BMA 방법론을 통해 각 지역별 최상의 분석 모델을 제시하고, 기존의 방법론으로 사용되고 있는 AR모형을 비교 분석하여 이를 통해 예측력을 향상시킬 수 있음을 보였다. 2007년 1분기부터 2010년 4분기까지의 정보를 토대로 11개 변수들의 조합으로 이루어진 2,047개의 모델들의 사후 확률을 지역별로 분석한 결과, 서울은 지가변동률(서울), 소비자물가지수, 시장금리, 주택담보대출금리, CD금리를 이용한 모델이, 부산은 GDP(명목)으로 구성된 모델이 확률적으로 가장 높은 것으로 나타났으며, Occam’s Window를 이용해 각 지역별 상위 모델군을 도출하였다.
BMS와 BMA를 통해 선정된 모델을 이용해 2011년 1분기부터 2014년 4분기까지 총 16기에서의 아파트 실거래가지수를 예측한 결과, 상대적으로 변동폭이 적은 부산에서의 예측력이 더 뛰어난 것을 확인할 수 있었다. 예측력의 비교를 위해 실제 아파트 실거래가지수와 예측한 값 간의 RMSE와 Average Rank를 사용한 결과, 예측력 부분에 있어 지역별로 차이가 나타났다. 먼저, 서울의 경우, RMSE와 Average Rank 모두 BMS, BMA, ARIMA 순의 동일한 결과를 나타냈다. 부산의 경우, RMSE와 Average Rank에서 차이가 있었는데, RMSE는 BMA, BMS, ARIMA 순으로, Average Rank는 ARIMA, BMS, BMA 순으로 나타났다. 이는 BMS, BMA가 기본적으로 변동의 폭이 큰 서울 지역의 아파트 실거래가지수를 중장기에 걸쳐 예측하는 데 있어 더 우월하고, 변동의 폭이 적은 부산 지역 역시 단기 예측에 있어 뛰어나다는 사실을 시사한다. 부산 지역의 경우 예측 기간이 길어질수록 ARIMA가 더 뛰어난 것으로 나타났는데, 이는 초기 20기내 정보를 통해 선정한 BMS와 BMA 모델이 단기 분석에는 유리하지만 장기 분석에서는 늘어난 시기에 부합하는 정보를 반영하고 있지 못하기 때문으로 보인다.
이에 본 연구가 기여할 수 있는 바는 크게 세 가지로 볼 수 있다. 먼저, 본 연구에서 제안하는 방법론을 통해 기존의 연구에서 발생하는 모델 선정의 불확실성 문제를 개선하였다. 기존의 계량경제학적 접근 방법의 경우, 보다 많은 변수들을 고려할수록 예측력을 향상시킬 수 있지만, 동시에 과적합(Overfitting) 문제에 직면할 수 있고, 변수들 간의 상관관계를 확인하기 위한 별도의 검정 절차를 거쳐야 한다. 그러나 본 연구는 기본적으로 변수 선정에서 야기되는 불확실성과 각각의 확률을 사전에 반영하고 있기 때문에 과적합 문제와 별도의 검정 없이 모든 변수들을 고려할 수 있다는 장점이 있다.
또한, 한 가지 모델에 의존하는 것이 아니라 모든 모델들을 확률적으로 고려함으로써 기존 대비 예측력을 향상시켰다. 기존의 연구에서는 주택 가격에 영향을 미치는 무수히 많은 요인들 중에 특정 변수들로 이루어진 하나의 모델을 선정하여 예측하기 때문에, 정보적인 측면에서 손실이 발생하게 된다. 하지만, 본 연구에서 제안하는 베이지안 프레임워크는 분석에 있어 각 변수들의 조합으로 이루어진 모든 모델들을 확률적으로 고려하고 있기 때문에 기존의 접근 방식보다 더 많은 정보로 분석을 수행할 수 있고, 보다 적은 오차 범위 내의 예측 결과를 도출할 수 있다.
뿐만 아니라, BMS와 BMA를 지역별로 비교 분석함으로써 지역별 특성을 반영한 분석 모형과 결과를 제시하였다. 기존의 연구에 따르면, 주택 가격에 있어 지역별 요인들이 미치는 영향이 크기 때문에 분석 모형 설정에 있어 지역적 특성을 고려하는 것은 매우 중요하다. 이에 주택 가격 변동이 비교적 큰 서울과 작은 부산을 비교 분석함으로써, 개별 지역에 적합한 모델들의 도출을 선정할 수 있었다.
본 연구는 모델 선정의 불확실성을 반영한 베이지안 접근법을 활용해 보다 개선된 주택 가격 분석 모형을 도출하는데 그 의의가 있으나, 이외에 몇 가지 한계점이 있다. 먼저, 주택 가격에 직접적인 영향을 미치는 여러 헤도닉적 요인들이 아닌 거시 경제학적 요인에만 초점을 맞추고 있어 실제 주택 가격에 미치는 효과들의 실증적인 분석을 반영하지 못하고 있으며, 이는 서울과 부산 두 지역에서 선정된 모델들이 지역적 특성을 잘 나타내지 못하는 결과를 초래하였다. 그러나 본 연구의 일차적인 목적은 모델의 불확실성을 감안한 새로운 예측 모형을 제안하고 이를 통해 기존 방법론 대비 예측력의 우수성을 보이는데 있기 때문에 데이터 수집이 용이하고 일반화가 가능한 거시 경제 변수의 사용을 우선적으로 고려하였다. 이러한 문제점은 향후 연구에서 “구”, “동” 단위의 헤도닉적 요인들과 거시 경제 요인들을 이용한 BMS, BMA 분석을 통해 보다 실질적인 주택 가격 예측으로 개선될 수 있을 것이라 생각된다.
또한, 본 연구에서 도출한 최적의 모형들이 실제 예측에 가장 적합하지 않다는 문제가 발생할 수 있다. BMS와 BMA는 연구자가 사용하는 변수의 수와 분석의 시기에 맞춰 최적의 모형의 종류와 수가 달라진다. 따라서, 만약 현 시점에서 아파트 매매가격지수 예측을 할 경우, 가용할 수 있는 모든 데이터로 미래의 가격을 예측해야하지만, 본 연구에서는 비교 분석을 위해 임의로 적은 데이터를 사용하고 있기 때문에 실제 예측에서 사용되는 최적의 모델과 차이가 발생한다. 즉, 본 연구에서 선정한 모형은 모델의 불확실성을 줄임으로써 예측력 개선을 보이기 위해 특정 기간을 대상으로 도출한 최적 모형으로 볼 수 있으며 분석 기간의 조절을 통해 실제 예측에 적합한 모형을 선정할 수 있다.