Ⅰ. 서론
2008년 글로벌 금융위기 이후 시작된 전세가의 상승은 2015년 현재까지도 지속되고 있는 반면 같은 기간 매매가는 상대적으로 정체되었다. 특히 2012년 6월부터 2013년 2월까지 주택 매매가격은 하락세를 보였지만 동기간 전세가격은 오히려 꾸준히 상승하였으며, 수도권의 매매가 대비 전세가 비율은 2012년 1월 54.1%에서 2015년 6월 64.3%로 약 10%포인트 이상 높아졌다. 전세가의 급등이 오늘날에만 국한되는 현상은 아니지만 최근의 변화는 기존과 다른 양상을 보인다. 2001년 전세가격이 1년 동안 16.4% 상승하여 매매가 대비 전세가 비율이 64.6%에 달했을 때는 전세수요가 매매수요로 전환되면서 안정을 되찾을 수 있었던 반면(최현일·임병진, 2011) 최근의 전세가 상승은 주택가격의 하락과 맞물려 매매수요를 기대하기 어렵다는 지적이 있다(윤종인, 2015). 또한 과거 아파트를 중심으로 발생한 전세가의 상승이 이제는 단독주택이나 연립다세대 주택 등 다른 유형의 주택에서도 발견되고 있으며, 전세가가 매매가에 육박하는 주택까지 등장하면서 상황은 과거보다 복잡하게 전개되고 있다.
이러한 주택시장의 변화는 과거의 주택시장과 공간적으로도 다른 양상을 보이고 있다. 수도권의 주택 매매가격이 보합 또는 하향안정세를 보이는 반면, 비수도권에서는 상승하는 추세가 나타난다. 반대로 전세의 경우 전국에서 상승하는 패턴을 보이나, 수도권에서의 급격한 상승세가 눈에 띈다(최두열, 2012). 이러한 주택시장의 공간적 변화 형태는 특정 지역에서 다른 지역으로 전이되는 현상으로 인식될 수 있다(김대원·유정석, 2015). 하지만 주택시장에서 특히 강남 지가가 다른 지역의 가격 변화에 영향을 주는지에 대해 다수의 연구가 진행되었으나, 영향력의 실재 여부 또는 전이 효과(spillover)의 발생 원인은 여전히 논쟁 중이다(이용만·이상한, 2004; 김경민, 2007; 서승환, 2007; 김호철·최창규, 2008).
한편, 주택시장에서의 매매가와 전세가의 관계에 관한 기존 연구들은 지역과 유형에 따라 분절된 주택시장을 단일 주택시장으로 가정하거나, 하나의 범주로 구분된 시장 내에서의 매매가와 전세가의 관계만을 분석했다는 점에서 한계가 있다. 하지만 최근 주택 시장의 변화를 살펴보면, 과거와 달리 아파트뿐만 아니라 다른 주택 유형에서의 전세가 역시 상당한 폭으로 변하고 있어 유형별 주택 가격 간에 발생하는 관계를 파악할 필요가 있다. 또한 주택 가격은 주변 지역과 밀접한 상호작용을 하고 있으므로 이를 고려해야만 미래 가격 변화에 대한 예측이 가능하다.
본 연구는 주택의 유형별 매매가와 전세가 간의 시공간적 상호작용 패턴을 파악함으로써 주택 가격 간 전이 효과를 탐색하고자 한다. 이를 위해 공간적 벡터자기회귀모형(spatial vector autoregression modell; SpVAR)을 활용하여 최근 전세가 상승이 두드러지는 수도권 주택시장의 시공간 상호작용 패턴을 분석할 것이다.
Ⅱ. 선행 연구
주택 시장에서의 상품 거래 형태는 매매와 임대로 구분할 수 있는데, 임대 방식의 하나인 전세의 가격은 주택이 갖는 고유한 특성으로 인해 결정되기도 하지만(김태호·이창무, 2006), 매매가격과의 관계 속에서 가격이 형성된다. Gallin(2008)은 주택의 임대료와 매매가격 간의 관계를 다음과 같이 정의하였다.
(식 1)에서 한 시점 에서의 임대료 는 주택의 현재가격 와 주택을 보유함에 따라 발생하는 사용자 비용(: 이자율, : 주택 보유세율, : 한계소득세율, : 유지비 및 감가상각율), 위험 프리미엄(), 현재 기대되는 미래 예상 자본 차익 의 함수로 구성된다. 즉, 임대료는 사용자 비용이 높을수록 상승하며, 주택의 미래가치가 높을수록 하락함을 의미한다.
이러한 주택의 매매와 전세가격 간 상호작용에 관한 연구는 꾸준히 진행되어 왔으나 분석시기에 따른 시기적 특수성과 분석 범위와 대상에 따른 인과적 방향성에 있어서는 여전히 이견이 많다. 우선 전세가에 의해 매매가가 결정된다고 본 황두현(1990)은 벡터자기회귀모델(vector auto- regression: VAR)을 통해 1986년 1월부터 1990년 4월까지의 주택매매지수와 전세가격지수를 비교한 결과, 지역과 주거형태에 관계없이 주거서비스에 대한 비용인 전세가격이 주택 매매가격을 형성해가고 있음을 밝혔으며, 박동국·천인호(2006)는 외환위기 이후의 주택 가격의 변동을 서울의 강남과 강북 지역을 사례로 살펴본 결과, 강남의 경우 전세가격이 매매가격에 선행하는 것으로 나타났다. 또한 전해정(2015) 역시 패널 VAR 모형을 이용하여 글로벌 금융위기 이후 전세가격이 주택 매매가격에 정적으로 영향을 미치고 있음을 밝혔다.
반면 매매가격이 전세가격을 선도한다는 입장의 연구로서 조주현·임정호(2004)는 VAR 모형을 바탕으로 전세의 매매 대체가능성에 주목하였는데, 매매가격에 의한 충격은 전세시장에 크게 미치는 반면 역의 경우는 크지 않음을 보였다. 임규채·기석도(2006)는 주택 유형별 매매가와 전세가를 변수로 하는 모델을 통해 아파트 매매가가 연립주택 전세가에 영향을 주고 있음을 밝혔다. 한편, 임재만(2004)은 주택 매매가격과 전세가격간 VAR모형을 기반으로 그랜저 검정을 수행한 결과 두 가격 간의 인과성을 인정하기 어려운 독립적인 재화로 보았다.
이상의 연구들의 공통점은 대부분이 단일 시장을 가정하거나 아파트와 같은 하나의 하위시장에서의 변화를 설명하고 있다는 점이다. 그 결과 주택 시장 내부에서의 다양한 상호작용과 다른 지역과의 관계를 포착하지 못하고 있다. 또한 계량경제학적 모델에만 근거하다 보니 현실에서 흔히 나타나는 주택 가격의 지역적 전이 효과를 포착하지 못한 한계를 지니고 있다.
이에 대한 대안적 접근으로 다수의 연구들(Giussani and Hadjimatheou, 1991; Stein, 1995; Pollakowski and Ray, 1997; Meen, 1999; Beenstock and Felsenstein, 2007; Kuethe and Pede, 2011; 이용만·이상한, 2004; 김경민, 2007; 서승환, 2007; 김대원·유정석, 2015)이 특정 지역의 주택 가격이나 임대료는 주변 지역의 매매가나 전세가와 공간적으로 상관되어 있음을 밝히고 있으나, 대개의 연구들이 매매가 또는 전세가 각각의 공간적 연관성만 다룰 뿐, 이들 두 가격 간의 공간적 상호작용은 제대로 반영하지 못하고 있다. 또한 주택 가격이 갖는 공간적 전이 효과를 살펴본 연구(김경민, 2007)에서도 통념상 원인으로 인식되는 하나의 지역이 설명 변수로 투입되어 해당 지역에 의한 효과만을 살펴보았을 뿐, 특정 지역의 주택 가격이 어떠한 원리로 다른 지역의 가격을 상승시키는지 제대로 설명하지 못하고 있다.
이는 주택가격의 시공간적 특성을 모두 반영하지 못한 기존의 시계열 분석 방법론의 한계라 할 수 있다. 예컨대, VAR모형은 전형적인 시계열 분석 방법으로 주택 가격의 공간적 특성을 간과하고 있으며, 공간적 단위를 포함하는 패널 VAR 역시 개별 공간의 이질성은 반영할 수 있었으나 공간 단위 간의 상호작용을 탐색하지 못하는 한계를 지닌다. 이러한 이유로 기존의 연구들은 지역 간에 발생하는 상호작용이 아닌 하위 시장 내부에서의 관계를 밝히거나(황두현, 1990; 임재만, 2004), 지역 시장 간 관계를 살펴본 연구에서도(임규채·기석도, 2006) 지역 간의 자기상관성은 반영하지 못하여, 모델에 의한 추정 결과가 과대 추정될 수 있다는 한계를 지니고 있다. 이에 따라 본 연구에서는 이러한 한계를 극복할 수 있는 대안적 분석 방법으로 시계열 분석을 공간적으로 확장한 공간적 벡터자기회귀모델에 주목하고자 한다.
Beenstock and Felsenstien(2007)에 의해 제안된 SpVAR은 시공간적 자기상관성을 동시에 다루는 모델로서 시계열적 의존성과 공간적 의존성만을 각각 필터링 하는 기존의 시계열 모델인 VAR과 공간 모델인 SAR(spatial auto- regression)과 차별성을 가지고 있다. 이러한 모델은 특정 변수의 과거 값과 주변 지역의 값이 해당 지역의 변수 값에 동시에 영향을 주는 경우에 유용한 방법이다.
SpVAR 모델은 기존의 시공간 모델인 STAR (spatiotemporal autoregression)(Cressie, 1993) 나 GTWR(Geographical and temporal weighted regression)(Huang et al., 2010)와 다른 차이를 보인다. STAR와 GTWR은 시공간 가중행렬을 통해 시공간적 자기상관성을 반영하지만, 단위가 다른 시간과 공간의 축이 임의의 모수들을 바탕으로 통합된 시공간에서의 가중행렬을 설정한다는 점에서 한계를 지닌다(Fotheringham et al., 2015a). 결국 시공간 상에서의 거리 설정은 모호할 수밖에 없으며, 다수의 연구(Pace et al., 1998; Sun et al., 2005; Huang et al., 2010; Wu et al., 2014; 박헌수, 2004; 전해정·박헌수, 2014)에서는 모델의 설명력 또는 예측력에 근거하여 적당한 모수를 설정할 뿐 해당 시공간 거리가 갖는 현실적인 해석은 제시하지 못하였다.
SpVAR모델의 경우 시공간 가중행렬을 사용하는 것이 아니므로 기존 시공간 분석 모델이 갖는 한계를 극복할 수 있으며, 각 시점 별 공간 가중행렬을 통해 시공간 자기상관을 반영할 수 있다. 이러한 SpVAR 모델의 기본 식은 다음의 (식 2)와 같이 표현할 수 있으며 각각의 기호는 <표 1>에 제시되어 있다.
| 기호 | 의미 |
|---|---|
| 변수 | |
| 지역 | |
| 시기 | |
| 관측값 | |
| 공간 가중된 관측값, | |
| 상수항 | |
| 일반 회귀 계수 | |
| 시계열 회귀 계수 | |
| 공간모델 회귀 계수 | |
| 지연된 공간시차 계수(lagged spatial lag coefficient) | |
| 오차항 |
SpVAR은 독립변수와 설명변수간의 시공간적 상호작용을 명시적으로 정의한 것으로서, 시기의 특정 지역 에서의 변수 값인 은 현재의 다른 변수()와 과거의 다른 변수들() 그리고 현재 주변지역으로부터 가중된 변수()와 과거의 주변 지역의 값()으로 설명될 수 있음을 의미한다. 이를 행렬형태로 전환하여 보다 간단하게 표기하면 (식 3)과 같이 나타낼 수 있다.
이 때, 는 지역의 수인 으로 구분된 인 관측값 벡터이며, 각 변수의 계수는 차원이 인 블록 대각 행렬(block diagonal matrix)이다. 그러나 이는 추정해야 하는 모수의 수()에 비해 식의 개수()가 부족하여 과소식별(under-identification)문제가 발생하므로 다음과 같이 축약된 수식으로 변환하여 추정할 수 있다(식 4).
축약된 방정식의 경우 각각의 변수에 대해 독립적인 회귀식으로 추정이 가능하나 시계열의 길이가 충분하지 못한 경우, 이를 하나의 블록으로 묶어 추정한다. 이 때, 각 블록에 속한 관측치의 개수는 지역별로 통합되어 개로 과소표본 문제가 해결할 수 있다. 이에 따라 낮은 자유도에 의해 발생할 수 있는 예측 부정확성을 해소할 수 있다.
축약된 SpVAR 모델에서 각 블록 안의 식들은 각 지역별 관계식들이므로 지역 간 발생하는 공간적 상관관계가 오차항에서 발현될 수 있기 때문에, 통상최소자승법 대신 외형적무관회귀법(seemingly unrelated regression: SUR)을 사용한다는 것이 특징적이다.
SpVAR 모델에서 변수에 의한 영향력을 파악하기 위해서는 일반적인 VAR 모델과 같이 충격반응분석이 추가적으로 필요하다. SpVAR 모델에서의 충격반응함수는 다음의 (식 5)와 같다.
(식 5)에서 는 초기 조건에 의한 상수항을 의미하며, 는 각 지역(N)별 변수(K)의 고유값(eigenvalues)들로서 의 절대값이 1보다 작다면 이 0으로 수렴하게 되어, 특정 지역에 외부로부터 가해진 충격은 만큼 다른 지역으로 확산 되는 것이다. 결국 SpVAR 모델에서 특정 시점에 한 지역에서 발생한 변화량(오차) 은 만큼의 관계를 갖고 있는 주변 지역에 누적적으로 영향을 미치며, 만큼 주변 지역의 과거값에 연쇄적으로 영향을 미치게 된다.
모델을 제시한 Beenstock and Felsenstien (2007)은 SpVAR 모델을 활용하여 1987년부터 2004년까지 예루살렘 인근 9개 지역의 주택 가격과 소득, 인구, 주택 재고량의 관계를 살펴본 결과, 예루살렘의 소득 상승이 주변지역 주택 상승에 영향을 미침을 보였다. 이 연구는 이전 방법들이 간과한 공간적 자기상관(spatial autocorrelation) 효과를 모델에 명시적으로 반영함으로써 공간적 파급 효과가 과대 추정되지 않는다는 장점을 보였다. 또한 이러한 방법을 차용한 Kuethe and Pede(2011) SpVAR을 이용하여 임금과 실업률을 바탕으로 미국 서부지역 11개 주들 간에 발생하는 주택 가격의 순환적 구조를 밝혔다. 이는 SpVAR 모델이 공간 더빈 모델(spatial Durbin model)과 달리 내생변수 간의 동태적 효과를 다루기에 적합한 모형이기에 가능하였다. 회귀분석에서 출발한 spatial Durbin model은 변수를 종속변수와 설명변수로 나누어 살펴보는 반면, VAR 모델에 기반을 두는 SpVAR는 변수를 내·외생성에 따라 구분하지 않기 때문에 경제이론에 근거한 가설 없이 실측값으로 현상을 살펴볼 수 있다는 장점이 있다.
변수 간 관계가 여전히 논쟁적인 주택의 매매가와 전세가의 관계를 살펴보고자 하는 본 연구에서는 공간 더빈 모델 보다는 SpVAR 모델로 살펴보는 것이 적합할 것으로 판단되어, 이를 바탕으로 과거 주변 지역에서의 가격변화 효과를 고려한 주택의 유형별 매매와 전세가격 간의 시공간적 상호작용을 살펴보고자 한다.
Ⅲ. 주택가격의 시공간적 특성 탐색
본 연구에 사용된 주택가격은 국토교통부가 제공하는 월별 실거래가 자료로 아파트, 연립다세대, 단독다가구 주택유형으로 구분한 후, 이를 각각 수도권 65개 시군구(도서지역인 옹진군 제외) 지역에 대하여 단위 면적 당 평균가를 계산하여 활용하였다. 월별 실거래가 자료는 다른 부동산 관련 지수들에 비해 시간적 범위가 짧다는 한계가 있으나, 공간적 단위의 선택에 있어 자유로우며 주택 종류와 거래 형태별로 지수가 아닌 가격 형태로 제공이 되어 보다 현실적인 해석이 가능하다(임재만, 2004). 또한 주택 거래 당사자가 직접 신고한 자료를 토대로 이상치(outlier)들이 관리자의 선험적인 근거에 의해 제거된 형태로 공개되고 있어 신뢰성도 높은 편이라고 볼수 있다. 분석의 대상이 되는 월별 실거래가는 주택 거래 신고가를 연면적(단독/다가구) 또는 전용면적(아파트와 연립다세대)으로 나눈 단위 가격(만 원/㎡)을 적용하여, 면적의 효과를 배제하였다.
주택 가격에 대한 기술통계량을 살펴보면 2011년 이후 전체적으로 매매가보다는 전세가의 상승이 두드러졌다. 주택 종류별 전세가와 매매가의 표준편차를 살펴볼 때, 모든 주택의 경우에서 전세가의 표준편차가 보다 크게 나타났다. 이는 시계열적 평균을 기준으로 등락의 폭이 보다 크게 나타났음을 보여준다(표 2).
시간에 따라 상이한 변동을 보이는 주택 가격의 시계열적인 특성을 통계적으로 검정하기 위하여 개별 변수별로 단위근 검정과 패널 단위근 검정을 실시하였다. 이는 증가 추세를 보이는 시계열을 SpVAR에 적용할 경우 과대오차로 인해 해석상의 문제가 발생될 수 있기 때문이다. 개별 시계열의 정상성은 ADF검정(Augmented Dicky-Fuller test)을 통해 평가하였고, 패널 단위근 검정은 Im et al.(2003)이 제시한 알고리즘을 기반으로 최대 시차를 8로 설정하여 실시하였다. 시차가 길수록 보다 다양한 경우의 수를 분석할 수 있지만, 8차 이후의 결과값에 큰 차이를 보이지 않아 8을 최대 시차로 설정하였다.
ADF검정 결과, 총 390개(65개 지역×6개 변수)의 시계열 자료 중 220개가 유의수준 10%에서 귀무가설인 비정상성을 기각하지 못하였다. 즉, 220개의 하위시장에서의 가격 변동은 일정한 추세(주로 상승하는 추세)를 보이고 있음을 반증한 것이다. 반면 가격을 1차 차분한 가격 변화량 자료에서는 약 11개의 비정상적 시계열이 도출되었다(표 3). 1차 차분 자료에서 보인 시계열적 정상성은 하위시장에서의 가격 변화율이 안정적인 것으로 해석할 수 있다.
| 변수 | 원가격 | 가격변화량(1차 차분) | |
|---|---|---|---|
| 전체 | 220 | 11 | |
| 아파트 | 전세 | 58 | 10 |
| 매매 | 54 | 0 | |
| 연립다세대 | 전세 | 25 | 0 |
| 매매 | 36 | 0 | |
| 단독다가구 | 전세 | 27 | 1 |
| 매매 | 20 | 0 | |
이를 보다 구체적으로 분석하기 위해 변수별로 살펴보면, 대부분의 지역에서 아파트 가격(전세와 매매)이 비정상성을 띄는 것으로 나타났다. 특히 아파트 전세가의 경우에는 1차 차분한 경우에도 10개 지역(경기 광명시, 경기 남양주시, 경기 의정부시, 경기 화성시, 서울 강동구, 서울 강서구, 서울 노원구, 서울 도봉구, 서울 성북구, 인천 서구)에서는 비정성상성을 띄고 있다. 하지만, 대부분의 다른 변수들에 대해서는 1차 차분에서 비정상성이 사라졌음을 확인할 수 있었다.
다음으로 실시한 패널 단위근 검정에서는 원가격과 가격 변화량(1차 차분) 모두 유의한 결과를 도출하였다(표 4). 그러나 이를 각 변수별로 나누어 살펴보게 되면 원가격의 경우 단독다가구의 전세가는 귀무가설인 비정상성을 기각하지 못하였다.
이를 종합해보면 2011년부터 2015년 6월까지 수도권 주택 가격은 일정한 추세를 갖고 증가하는 패턴을 보이고 있다. 전체 패널로 보았을 때 이러한 비정상성이 두드러지지는 않았지만, 아파트 전세가와 같은 개별 시계열 자료에서는 추세를 무시하기 어려운 패턴을 보이고 있어 가격 자체를 SpVAR 모델에 직접 적용하기 어렵다. 그러나 1차분한 가격변화량의 경우 패널은 물론 개별 시계열에서 정상성을 띄고 있어 SpVAR 모델에 활용하기 적합한 것으로 판단된다.
시공간 모델인 SpVAR는 분석 자료에 시간적 효과뿐만 아니라 공간적 효과가 존재함을 가정한다. 공간적 효과 중 공간적 의존성은 주변지역의 값이 특정지역의 값에 영향을 미치는 현상으로 정의할 수 있다. 주택은 한 지역이 동시에 개발되고, 가격에 영향을 미치는 근린 요소를 공유하면서도 주변 지역에 미치는 외부효과를 발생시키고 가격의 기준이 주변 시세로 책정되기 때문에 공간적으로 의존성이 높은 재화이다(Fotheringham et al., 2015b).
주변지역과의 공간적 의존성을 측정하기 위해서는 특정 지역에 대한 적절한 근린을 정의하는 것이 선행되어야 한다. 대개 근린은 공간 가중행렬(spatial weight matrix)의 형태로 표현되는데 본 연구에서는 경계를 공유하는 시군구의 집합으로 정의하였으며, 2010년 행정구역을 기준으로 모든 시기에 동일한 가중행렬을 설정하였다. 이러한 공간 가중행렬을 바탕으로 대표적인 전역적 공간적 자기상관 측정치인 Moran’s I와 이변량 Moran’s I를 적용하여 주택 유형별 매매가와 전세가의 공간적 자기상관성을 살펴보았다. <표 5>에서 대각행렬은 각 변수별 평균 변화량의 공간적 자기상관지수로 각 변수별 Moran’s I를 의미하며, 하삼각행렬은 각 변수 간의 이변량 Moran’s I값을 나타낸다. 이 때, 각 주택별 매매가의 변화량은 공간적 자기상관이 나타나고 있지 않지만, 전세가의 변화량은 유의한 수준의 비교적 높은 공간적인 자기상관을 나타내고 있다. 이는 전세가의 변화량이 공간상 인접한 지역에서 유사하게 나타나고 있으며, 주변지역으로 영향을 미치고 있음을 의미한다. 뿐만 아니라 아파트 전세가 상승은 주변지역의 아파트 매매와 연립다세대의 전세가, 매매가, 단독주택의 전세가 상승에 영향을 주고 있음을 알 수 있다. 특히 아파트 전세와 연립다세대 주택의 전세는 상당한 공간적 자기상관을 보이고 있다. 예를 들어, 강남구 아파트 전세가의 상승은 주변 지역(서초구)의 연립다세대 주택의 전세가 상승과 함께 나타나고 있다고 볼 수 있다. 이는 두 변수 간의 시간적 선후행 관계는 알 수 없으나 공간적으로 밀접한 상호작용, 즉 공간적 자기상관성이 존재함을 의미한다.
Ⅳ. 주택 유형별 매매-전세가격 상호작용 분석
본 연구에서 제시한 수도권 주택 유형별 매매-전세가격의 SpVAR 모델은 (식 6)과 같다.
단,
이 식은 각각 52개(T=52)의 사례수와 12개(시차변수 6개, 지연된 공간시차 변수 6개)의 설명변수가 있는 방정식 390개(65개 지역, 6개 변수)를 포함하고 있다. 즉, 각각의 변수별 블록에는 65개 지역의 시계열자료가 통합되어, 총 3,380개(N=65, T=52)의 사례수를 바탕으로 블록별 SUR 추정이 가능하게 되었다. 전 지역에서의 변수 간의 관계는 동질적으로 가정하며, 한 지역의 특정 변수에 영향을 미치는 다른 지역의 변수는 전역적인 변수 간 관계로 가정한다. 예를 들어, 강남구 아파트 전세가와 매매가의 관계는 전기의 서초 또는 송파구의 관계와 다를 수 있지만, 이를 수도권 전역에서의 전세가와 매매가 간의 관계로 간주한다.
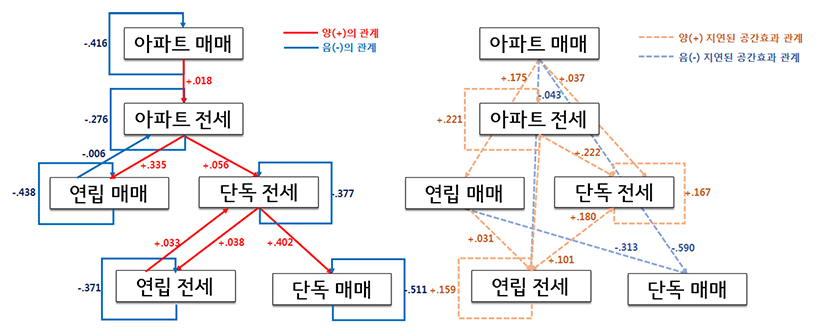
각 블록별로 추정된 표준화 계수는 <표 6>과 같다. 단순히 주택 유형별 가격에 따른 모델이기 때문에 모델의 설명력이 높지는 않으나, 변수들의 관계에서는 몇 가지 주목할 만한 결과가 도출되었다. 우선 아파트 전세의 가격 변화량은 해당 지역의 전기 전세가 변화량과는 반비례(-0.276)하지만 전기의 주변지역 전세가 변화량에는 비례(0.221)한다. 이는 직관적인 인식과 부합하는 결과로 지난달에 전세가가 급등할 경우, 시장에서 이를 비싸다고 여겨 소비자들의 수요가 둔화됨에 따라 가격 변화량이 낮아지는 현상을 보이기 때문이다. 그러나 주변지역의 영향력이 포함된 가격의 전기 값이 긍정적인 영향을 미친다는 것은 결국 주변지역의 전세가 상승이 해당지역의 전세가 상승에 영향이 있으며, 주택 가격이 주변으로 시차를 두고 확산해 나가고 있음을 뒷받침하는 결과로 볼 수 있다. 또한 아파트 전세가의 변화는 아파트 매매가 변화량에 비례(0.018)한다. 이는 매매가 상승폭이 가파를 경우, 공급자는 전세 물량을 매매로 전환하고자 하며 소비자는 아파트를 구매하는 대신 전세를 선택하게 되기 때문에 전세 물량이 수요에 비해 공급이 부족해져 가격이 상승하는 것으로 사료된다. 반면 아파트 매매의 경우, 아파트 전세와의 관계가 유의하지 않아 아파트 전세가 변화가 매매가 변화에 영향을 준다고 보기 어렵다. 이는 국내 아파트 시장에서 매매가 임대의 상급재라는 가설을 뒷받침하는 결과라 할 수 있다. 게다가 아파트 전세가의 상승폭이 커질 때, 연립다세대 매매가 역시 상승하게 되는데 이는 아파트에 대한 선호 등 가격 이외의 요소에서 발생하는 상급재적 요소로 인한 결과로 파악된다. 한편, 기간 내 연립다세대의 평균 매매가격은 아파트의 평균 전세가를 상회하여 아파트 전세가 연립다세대 매매의 상급재로는 보기 어렵다. 그러나 우리나라의 주택 인식 상 아파트가 연립주택에 비해 고급재화라는 인식이 있어 소유형태와 무관하게 아파트에 거주하는 것을 선호한다. 이러한 인식으로 인해 아파트 전세가가 빠르게 상승하게 되면, 이에 대한 대체 재화로 연립다세대 주택을 선택하기 때문에 그의 매매가 역시 빠르게 상승할 수 있음을 시사한다. 또한 연립다세대의 매매가와 달리 전세가는 다른 재화에 비해 주변에 의한 영향을 강하게 받는 것으로 나타났다. 특히 주변 지역의 아파트 전세가의 상승에 상대적으로 큰 영향을 받는 것으로 나타났는데, 이는 최근의 아파트 전세가 상승이 주변 지역의 연립다세대 주택으로 전이되는 것을 실증적으로 보여주는 결과라 할 수 있다. 즉, 높아진 아파트 전세를 대체할 재화를 주변 지역의 비교적 저렴한 연립다세대 주택으로 판단하는 것이며 이 과정에서 미래가치가 아닌 주택의 사용가치를 더 고려한 의사결정이 이뤄진다고 볼 수 있다.
<그림 1>은 이상의 관계를 보다 이해하기 쉽게 표현한 모델이다. 이를 살펴보면, 아파트 매매는 가장 상위 재화로 위치하며 자기회귀적인 영향만 받을 뿐 다른 변수에 의해 설명되지 않고 있다. 결국 아파트 매매 가격은 다른 주택 종류의 가격에 대해 독립적으로 결정되며, 부적 피드백 작용을 받으며 상승폭이 제한된다. 이렇게 결정된 아파트 매매 가격은 아파트 전세시장에 양의 영향을 준다. 비록 큰 영향력은 아니지만, 매매 가격의 증가 폭이 상승할 때, 아파트 전세 가격 상승률도 높아지는 것을 확인할 수 있다. 대신, 높아진 아파트 전세가를 대체하기 위한 수단으로 연립주택을 매매하거나 단독주택을 전세로 구하는 경우가 발생함을 확인할 수 있다. 또한 아파트 전세가의 상승은 주변 지역의 다른 재화에 영향을 주는데, 특히 연립주택의 전세가는 다른 재화에 비해 상대적으로 큰 영향을 받는다. 이러한 결과는 최근 전세가의 상승이 아파트 가격의 상승을 이끌지는 못하고 있지만, 주변 지역으로 점차 확산되어 특히 연립주택의 전세가에 영향을 미치는 현상을 설명할 수 있는 근거가 될 수 있을 것으로 판단된다.
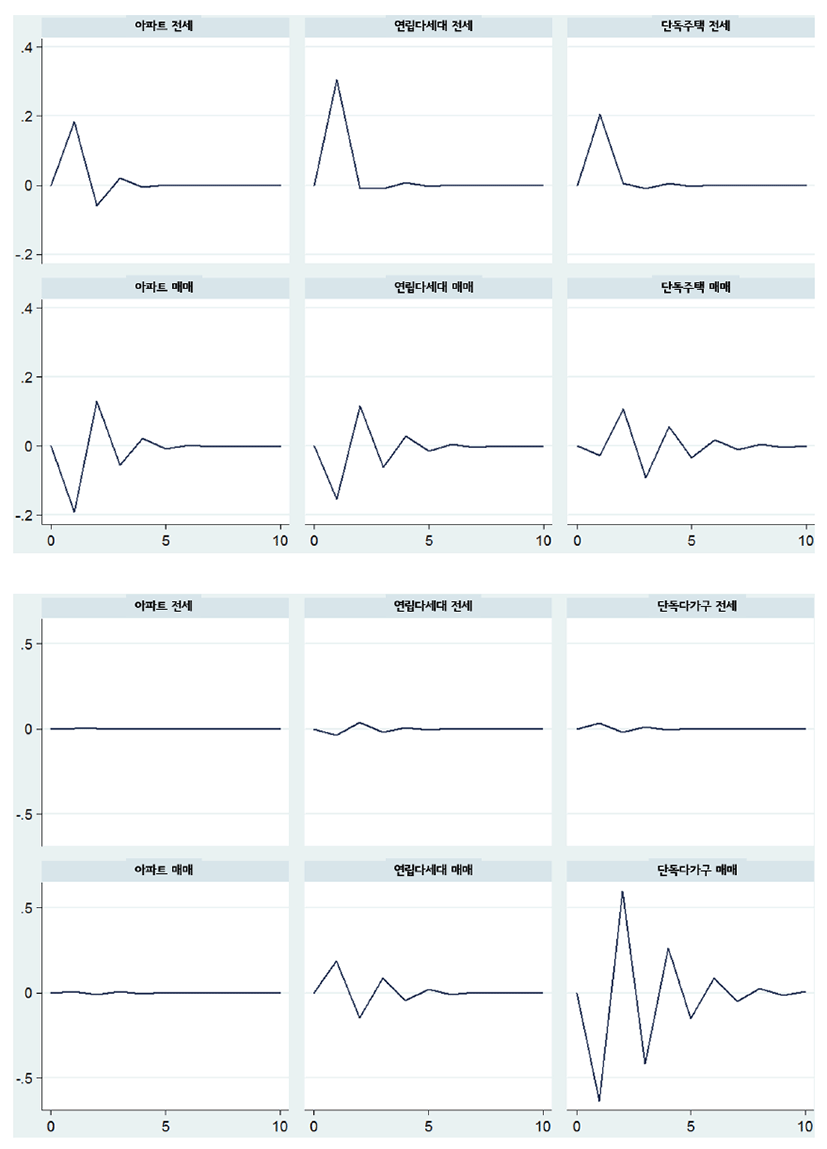
이러한 주변지역의 아파트 가격에 의한 전이 효과를 보다 면밀히 살펴보기 위해 충격반응분석을 수행하였다. 그 결과, 아파트 매매가와 아파트 전세가의 영향력은 현저한 차이가 있음을 알 수 있다. <그림 2>는 시간이 흐름에 따라(x축) 변하는 충격에 반응하는 정도(y축)를 나타낸 그래프로서, 한 변수가 외부적인 요인에 의해 1단위 변할 때 다른 변수가 어느 정도 변하는지를 보여준다. <그림 2>의 상단에 있는 그래프는 주변 지역의 아파트 전세가가 1단위 상승하였을 때, 다른 변수들의 반응 정도를 보여주는 것으로서 아파트 전세가는 1기 후(1달 뒤)에 바로 상승하나, 이후 상승효과의 반대급부로 하락하는 경향을 보인다. 이는 아파트 전세가의 공간적 자기상관성이 시차를 두고 영향을 주는 전이 효과로 볼 수 있다. 즉, 주택 가격이 주변 시세를 참고하여 책정되는 공간적 의존성의 산물이라는 Fortheringham et al.(2015b)의 설명에 부합하는 결과이며, 공간적 의존성이 가격에 반영되는 과정에서 발생하는 시차를 의미한다. 또한 연립다세대 전세가의 반응량은 다른 변수들에 비해 상대적으로 크게 나타났으며, 단독다가구의 전세가 역시 빠르게 반응하는 것으로 나타났다. 이러한 결과는 최근 아파트 전세가 상승에 의한 대체 재화의 상승을 다시 한 번 보여주는 결과라 할 수 있다. 그러나 이러한 변화는 1기 이후 거의 소멸되는 것으로 나타나 아파트 전세가에 상승에 의한 가격 상승은 장기적 요인이 아님을 확인할 수 있다. 즉, 전세가 상승이 지속되지 않는다면, 대체재화의 가격 상승도 제한될 것으로 예상할 수 있다.
한편 <그림 2>의 하단에 있는 그래프를 통해, 주변지역의 아파트 매매가는 단독주택의 매매를 제외한 다른 유형의 주택 거래에 대해 거의 영향을 미치지 않고 있음이 다시금 확인되었다. 다만, 단독주택 매매가의 큰 변이는 주목할 만한데, 다른 주택 유형보다 단독주택의 주변지역 아파트 매매가에 가장 민감하게 반응함을 보여준다. 이러한 현상은 향후 추가적인 연구를 통해 그 원인에 대한 고찰이 필요한 것으로 보인다.
SpVAR를 통해 도출한 수도권 주택시장의 가격 추정 및 모델의 타당성을 평가하기 위하여 공간시차 항이 없는 패널 VAR 모델의 결과와 비교하였다. 추정의 정확성은 모델에서 발생한 오차에 대해 시군구 단위의 평균절대오차(mean absolute error: MAE)와 평균제곱근오차(root mean squared error: RMSE)를 산출하여 평가하였으며, 모델의 타당성을 추정모델에 사용되지 않은 자료(2015년 7월과 8월)에 대한 모델의 예측 결과를 교차평가하였다.
<표 7>은 각 모델 별 MAE와 RMSE의 결과를 보여주는 것으로, 추정에 있어서 패널 VAR 모델의 결과가 약간 우세해 보이나 이는 통계적으로 유의한 차이를 보이지 않았다. 교차 타당성 평가 역시 2015년 8월 자료에 대해 SpVAR가 다소 개선된 측면을 보이나, 두 모델 간 유의한 차이가 발생하지 않았다. 이러한 오차 크기 측면에서의 한계를 보완하기 위해 가격 변화의 방향성 예측 결과를 비교하였다. 왜냐하면 오차의 절대값이 작은 경우 실측값과 예측값의 부호가 다르더라도 그 값은 크지 않게 나오는 반면, 절대값이 큰 경우 일반적인 추세에서 크게 어긋나 있지 않아도 큰 오차를 보이기 때문이다. 각 모델에서 예측한 결과가 실제 관측값과 같은 부호를 갖는다면, 이를 예측 ‘성공’으로 정의하고 다른 부호일 경우 예측 ‘실패’로 정의하였다.
그 결과 <표 8>에서와 같이 2015년 7월의 경우, 두 모델 모두 매우 높은 비율(58%)로 실측값과 같은 변화 방향을 예측하였지만 8월에는 다소 하락한 것으로 나타났다(37%). 그러나 각 모델 간 방향성 예측의 정확성의 비율을 의미하는 승산비(odds-ratio)의 경우, 7월에는 1057이었지만 8월에는 148로 대폭 상승하였다 대응표본에 있어서 두 모델 간 방향성 예측에서의 정확성 차이는 SpVAR에서 약간 우세한 편이지만, 교차 타당성 평가에 있어서는 SpVAR의 결과가 패널 VAR에 비해 상당히 정확함을 의미한다 이러한 차이는 McNemar 검정을 통해서도 확인할 수 있다 귀무가설을 두 모델 간 예측 결과가 맞을 확률이 같다고 두었을 때, 7월의 경우 이를 기각하지 못하지만 8월은 이 귀무가설을 기각하는 결과가 나타났다.
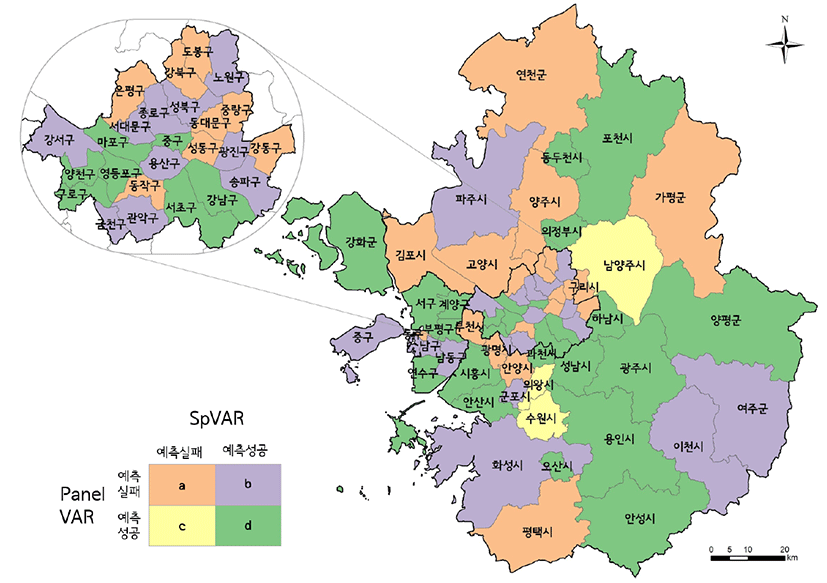
여러 변수들에 대한 방향성 예측 결과 중, 주변지역의 변수에 가장 많은 영향을 받는 연립다세대 주택의 8월 전세가의 공간적 분포를 살펴보면 <그림 3>과 같다. 우선 24개 지역에서는 두 모델 모두 실제와 같은 변화 방향이 예측된 반면(d지역), 경기 북부를 중심으로 한 지역에서는 두 모델 모두 예측에 실패하였다(a지역). 이는 가격 변화량이 크지 않은 경기 북부지역에 대해 다수의 변수에 의한 과대 추정된 결과로 판단된다. 한편, 패널 VAR 모델만 정확하게 방향성을 예측한 지역은 의왕시, 수원시, 남양주시가 있다(c지역). 이 지역들은 주변 지역의 주택 가격 변화로 가격 변화량을 예측하는 것이 부정확함을 의미하며 이는 해당 지역의 연립주택 전세가 변화는 주변 지역과 무관하게 나타나는 현상임을 유추할 수 있다. 반대로 SpVAR 모델에서만 방향성 예측이 맞은 19개 지역(b지역)은 주변 주택 가격 변화로 연립주택 전세가의 변화 방향이 예측됨을 의미한다. 연립다세대 전세가가 주변 지역에 민감하게 반응하고 있는 충격반응분석 결과(그림 2)를 상기해 보면, 해당 지역의 연립다세대 전세가는 주변 지역의 아파트 전세가에 의해 변한다고 유추해 볼 수 있다. 왜냐하면 패널 VAR 모델은 SpVAR 모델과 달리 지연된 공간시차 항이 없어, 모델의 결과가 부정확하다면, 주요 설명 변수가 누락된 것으로 볼 수 있기 때문이다. 또한 SpVAR 모델의 추정 결과(표 6), 표준화된 지연된 공간시차 계수 값 중 아파트 전세가가 가장 크기 때문에 상대적으로 영향력이 크다고 볼 수 있다.
이러한 공간적 분포 패턴은 아파트 전세가와 연립다세대 전세가의 전이 효과가 일부 수도권 지역에서 나타나고 있음을 보여주고 있으며, 특히 최근 전세가 상승의 진원지로 지적되고 있는 강남구와 서초구의 아파트 전세 가격이 인근 지역(관악구, 용산구, 광진구, 송파구)으로 시차를 두고 전이되는 과정에서 발생한 것으로 판단된다.
Ⅴ. 결론 및 논의
본 연구는 주택의 유형별 매매가와 전세가 간의 시공간적 상호작용 패턴을 파악하기 위해 공간적 벡터자기회귀모델(SpVAR)을 적용하였으며, 최근 수도권 주택 시장에서 발생하고 있는 주택 가격의 전이 효과를 실증적으로 검증하였다.
그 결과 1기 전 인접 시군구의 아파트 전세가 상승은 모든 유형의 전세가에 양의 영향을 미치는 것으로 나타난 반면, 아파트 매매가의 경우 그 영향이 미미한 것으로 나타났다. 특히 아파트 전세가의 상승은 주변 지역 연립다세대 주택 전세가에 상대적으로 큰 파급효과를 불러일으켜, 아파트 전세가 상승이 주변 지역의 연립 주택 전세가격으로 전이되고 있음을 확인할 수 있었다. SpVAR 모델을 이용한 주택 가격의 예측 결과를 살펴보면 기존의 패널 VAR 모델에 비해 정확성이 소폭 개선되었음을 확인할 수 있다. 예측 오차의 절대량으로 비교할 경우 두 모델에 유의한 차이는 없었으나, 가격의 상승 혹은 하락과 같은 가격 변화량의 방향을 예측하는 데 있어서는 SpVAR 모델이 유효한 것으로 나타났다.
본 연구는 주택 유형별 매매, 전세가격 간 시공간적 상호작용을 실증적으로 보여주고 있다는 점에서 의의가 있지만, 제시한 모델이 기존의 모델에 비해 압도적으로 개선된 방법임을 검증하지 못한 한계가 있다. 이는 분석의 두 축인 시간과 공간 측면, 그리고 변수의 제약에서 원인을 찾아 볼 수 있다. 첫째는 시간적 측면에서 분석의 시간적 범위가 크지 않다는 한계가 있다. 시계열적 변화를 추적하고 설명하는데 있어, 4년 6개월이라는 시간적 범위는 다소 제한적이라 할 수 있다. 반면, 공간적 측면에서는 분석의 공간적 단위가 비교적 크게 설정되었다는 한계가 있다. 기존의 연구들에서도 주로 활용된 시군구 단위는 사실 상당히 넓은 범위로서 주택 가격의 공간적 효과가 상쇄될 수 있는 크기이다. 즉, 시군구 간 주택 가격의 공간적 의존성이 높지 않아 SpVAR 모델로 추정한 결과가 이를 고려하지 않은 모델과 큰 차이를 보이지 않은 것으로 판단된다. 이는 수정가능한 공간단위의 임의성 문제(modifiable areal unit problem : MAUP)와도 관련되는 것으로 추후 공간 단위를 보다 세밀한 수준으로 나누어 살펴볼 필요성을 함의한다. 또한 모델에서 살펴본 변수들은 유형별 주택 가격으로 실제 주택가격에 영향을 줄 수 있는 외생변수들이 고려되지 않았다는 점에서 전체적인 예측력 개선이 어렵다는 한계가 노출되었다.
그럼에도 불구하고 본 연구를 통해서 현재 수도권 주택 시장에서는 특정 재화의 가격변화가 공간적 상관성에 의해 설명될 수 있음을 통해 주택 가격의 전이 효과가 나타나고 있음을 확인할 수 있었으며, 이러한 효과가 일관적으로 나타나는 것이 아니라 주택 유형에 따라 다르게 전개되고 있음을 알 수 있었다. 이러한 연구의 결과는 주택 가격 변화의 과정에서 주변 지역의 영향력을 판단할 수 있는 기초자료로 활용될 수 있으며 나아가 전세가 상승에 대한 대응 정책이 특정 지역에 국한되거나 공간적인 상호작용 관계를 간과해서는 안된다는 정책적 시사점을 내포하고 있다.